机器学习中的前4个图表
机器学习 | 绘图 | Python
掌握机器学习最重要的可视化技巧的实用指南
在机器学习的动态世界中,可视化起着至关重要的作用。它们是数据讲述复杂故事的无声叙述者。
尤其在机器学习领域,数据可视化对于更好地理解模型的基本结构和更好地解释结果质量具有更为重要的作用。
在本文中,我们将深入探讨任何机器学习爱好者必须掌握的五个关键绘图。
绘图1:拐点图
拐点图是用于确定聚类算法(例如K-Means)中最佳聚类数的优秀工具。
正如名称所示,该图通常具有一个明显的弯曲点(即拐点),其指示添加更多聚类会导致更差的聚类分离和较差的结果的“甜点”。
此图对于确保我们从数据中提取有意义的聚类而不是过度拟合或欠拟合至关重要。
在需要我们指定预先确定的聚类数的无监督算法(如K-Means)中,拐点方法对于帮助我们确定选择的最佳聚类数至关重要。
下面是一个生成拐点图的简单Python代码片段:
from sklearn.cluster import KMeansfrom sklearn.datasets import make_blobsimport matplotlib.pyplot as plt# 生成样本数据data, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)distortions = []for i in range(1, 11): km = KMeans(n_clusters=i, random_state=0) km.fit(data) distortions.append(km.inertia_)# 绘制拐点plt.plot(range(1, 11), distortions, marker='o')plt.xlabel('聚类数')plt.ylabel('失真程度')plt.title('拐点方法显示最佳聚类数')plt.show()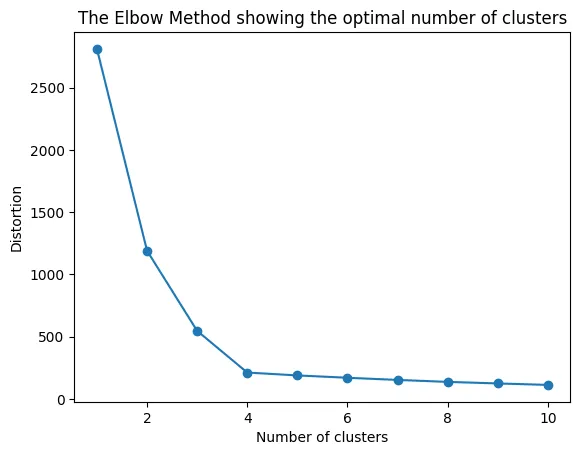
在上面的图中,我们可以看到我们正在绘制失真度与聚类数之间的关系。
失真度是特定数据点与其簇中心之间的欧几里得平方距离。通常也使用惯性(即平方距离的总和)。
这里的目标是选择完美的折衷方案。
我们希望获得低失真度/惯性值以获得紧密的簇内相似性。但同时,我们希望每个单独的簇尽可能独特。
因此,完美的情况将是非常低的簇内相似度,但是非常高的簇间相似度。
我们通过取拐点处的点来近似这个甜点。在上面的图中,我们可以选择3或4个簇。
拐点处的点确保我们具有低失真度值,而不具有饱和的聚类数。
绘图2:AUROC曲线
接收器工作特征(AUROC)曲线是主要用于二元分类任务的基本绘图。
它衡量了ROC曲线下的整个二维区域,该曲线绘制了不同阈值下的真阳性率(敏感性)与假阳性率(1-特异性)。
AUROC值的范围从0.5(基本上是随机模型)到1.0(完全具有区分性的模型),帮助我们无论阈值如何都可以量化模型性能。
from sklearn.metrics import roc_curve, aucfrom sklearn.datasets import make_classificationfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionimport matplotlib.pyplot as plt# 生成二元分类数据集。X, y = make_classification(n_samples=1000, n_classes=2, weights=[1,1], random_state=1)# 分成训练/测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=2)# 训练逻辑回归模型model = LogisticRegression(solver='liblinear')model.fit(X_train, y_train)# 预测概率probs = model.predict_proba(X_test)# 只保留正结果的概率。probs = probs[:, 1]# 计算ROC曲线fpr, tpr, thresholds = roc_curve(y_test, probs)# 计算接收器工作特征曲线下的面积(AUROC)roc_auc = auc(fpr, tpr)# 绘制ROC曲线plt.plot(fpr, tpr, label='ROC曲线(面积=%0.2f)' % roc_auc)plt.plot([0, 1], [0, 1], 'k--') # 随机预测曲线plt.xlim([0.0, 1.0])plt.ylim([0.0, 1.0])plt.xlabel('假阳性率或(1-特异性)')plt.ylabel('真阳性率或(敏感性)')plt.title('接收器工作特征曲线')plt.legend(loc="lower right")plt.show()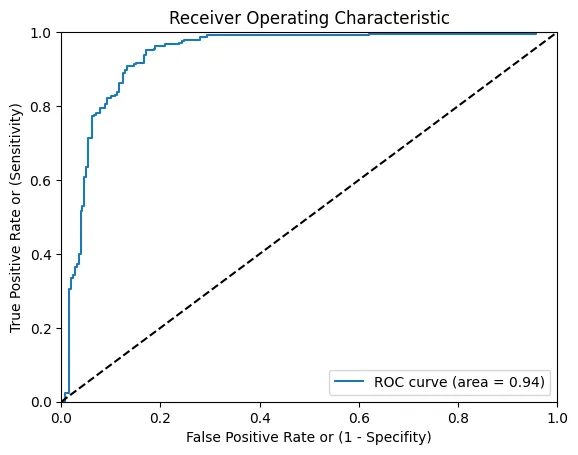
在上面的图中,我们看到了我们的基准线(黑色虚线)。
理想情况下,任何模型都应该尽可能远离基准线,并朝着图的上半部分(即高真正率但低误报率)方向发展。
图3:累计解释方差
累计解释方差图在主成分分析(PCA)中非常重要——这是一种用于降维的技术。
这个图帮助我们确定我们应该选择保留多少个主成分,同时仍然保留原始方差的大部分。
from sklearn.decomposition import PCAfrom sklearn.datasets import load_irisimport matplotlib.pyplot as pltimport numpy as np# Load the datairis = load_iris()X = iris.datay = iris.target# Compute PCApca = PCA(n_components=4)X_pca = pca.fit_transform(X)# Plot the explained variancesfeatures = range(pca.n_components_)explained_variance = np.cumsum(pca.explained_variance_ratio_)plt.bar(features, explained_variance, alpha=0.5, align='center', label='individual explained variance')plt.step(features, explained_variance, where='mid', label='cumulative explained variance')plt.ylabel('解释方差比率')plt.xlabel('主成分')plt.legend(loc='best')plt.tight_layout()plt.show()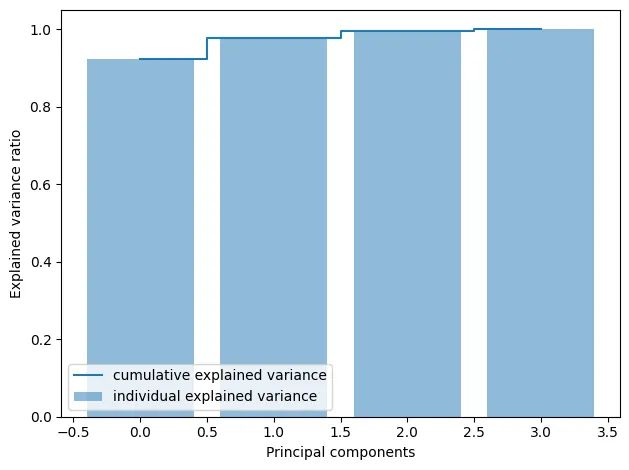
在这里没有具体的值要选择,但是通常的经验法则是尽量保留解释方差比率为0.8。
这个过程类似于图1中的拐点方法。我们每次运行各种步骤,每次增加主成分的数量。
然后,使用解释方差图,我们可以确定需要保留原始方差的最小主成分数量。
图4:精度-召回曲线
精度-召回曲线是二元分类任务的另一个重要工具,类似于AUROC。
它说明了分类器在标签负样本不被误判为正样本的能力(精度)和分类器发现所有正样本的能力(召回)之间的权衡。
当处理不平衡数据集时,这个图尤其有用。
from sklearn.metrics import precision_recall_curvefrom sklearn.metrics import aucfrom sklearn.datasets import make_classificationfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionimport matplotlib.pyplot as plt# Generate a binary classification dataset.X, y = make_classification(n_samples=5000, n_classes=2, weights=[1,1], random_state=1)# Split into train/test setsX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=2)# Train a logistic regression modelmodel = LogisticRegression(solver='liblinear')model.fit(X_train, y_train)# Predict probabilitiesprobs = model.predict_proba(X_test)# keep probabilities for the positive outcome onlyprobs = probs[:, 1]# Compute the precision-recall curveprecision, recall, thresholds = precision_recall_curve(y_test, probs)# Compute the area under the precision-recall curvepr_auc = auc(recall, precision)plt.plot(recall, precision, label='PRC curve (area = %0.2f)' % pr_auc)plt.xlabel('召回率')plt.ylabel('精度')plt.title('精度-召回曲线')plt.legend(loc="lower right")plt.show()
总结
总之,这四个图是数据科学家工具箱中的强大工具。
通过明智地使用这些可视化工具,您可以从数据中提取有意义的见解,诊断模型的性能,并有效地传达您的发现。
掌握这些图表不仅有助于理解手头的数据,还有助于对模型选择和超参数调整做出明智的决策。因此,请随时使用这些可视化工具,让您的机器学习故事展开。
您喜欢这篇文章吗?每月支付5美元,您可以成为会员,解锁对小猪AI的无限访问。您将直接支持我和您在小猪AI上喜爱的其他作者。非常感谢您的支持!
使用我的推荐链接加入小猪AI – David Farrugia
获取对所有我的⚡高级内容和小猪AI上的所有内容的独家访问权,无限制。通过为我购买…来支持我的工作
david-farrugia.medium.com
想要联系我吗?
我很乐意听取您对主题或任何人工智能和数据方面的想法。
如果您希望联系我,请发送电子邮件至[email protected]。
领英






