理解贝叶斯市场营销组合建模:先验规范的深入研究
使用Google的LightweightMMM探索模型规范
贝叶斯市场混合建模受到越来越多的关注,尤其是随着开源工具LightweightMMM(Google)或PyMC Marketing(PyMC Labs)的最新发布。虽然这些框架简化了贝叶斯建模的复杂性,但用户仍然需要了解基本的贝叶斯概念,并能够理解模型规范。
在本文中,我以Google的LightweightMMM为实际例子,展示了该框架先验规范的直觉和含义。我使用Python和scipy库演示了先验样本的模拟。
数据
我使用Robyn在MIT许可下提供的数据。
数据集包括208周的收入(从2015年11月23日到2019年11月11日),其中包括:
- 5个媒体支出渠道:电视_S,户外_S,印刷_S,Facebook_S,搜索_S
- 2个媒体渠道也具有曝光信息(印象、点击):facebook_I,search_clicks_P
- 没有支出的有机媒体:newsletter
- 控制变量:events,holidays,竞争对手销售(competitor_sales_B)
LightweightMMM模型规范
LightweightMMM模型的规范定义如下:
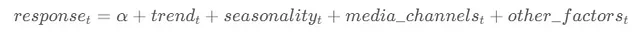
该规范表示一种加性线性回归模型,该模型解释了特定时间点t的响应(目标变量)的值。
让我们逐个解释方程中的每个组成部分:
- α:该组件表示截距或响应的基线值。当所有其他因素为零时,它是响应的预期值。
- trend:该组件捕获响应随时间的增长或下降趋势。
- seasonality:该组件表示响应的周期性波动。
- media_channels:该组件说明媒体渠道(电视、广播、在线广告)对响应的影响。
- other_factors:该组件包括任何对响应有影响的其他变量,如天气、经济指标或竞争对手活动。
下面,我将逐个详细介绍每个组件,并解释如何解释先验规范。提醒一下,先验分布是在没有任何关于底层数据的知识的情况下假定某个参数的分布。
截距

截距定义为遵循标准差为2的半正态分布。半正态分布是一种连续概率分布,类似于正态分布,但仅限于正值。该分布特征为一个参数,即标准差(尺度)。半正态分布意味着截距只能获得正值。
以下代码生成截距的先验分布样本,并可视化标准差为2的半正态分布的概率密度函数(PDF)。有关其他组件的可视化,请参阅Github repo中的附带源代码。
from scipy import statsscale = 2halfnormal_dist = stats.halfnorm(scale=scale)samples = halfnormal_dist.rvs(size=1000)plt.figure(figsize=(20, 6))sns.histplot(samples, bins=50, kde=False, stat='density', alpha=0.5)sns.lineplot(x=np.linspace(0, 6, 100), y=halfnormal_dist.pdf(np.linspace(0, 6, 100)), color='r')plt.title(f"Half-Normal Distribution with scale={scale}")plt.xlabel('x')plt.ylabel('P(X=x)')plt.show()
趋势
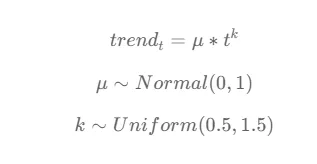
趋势被定义为时间t和趋势值之间的幂律关系。参数μ代表趋势的振幅或大小,而k控制趋势的陡峭程度或曲率。
参数μ从均值为0,标准差为1的正态分布中获得。这意味着μ遵循以0为中心,标准差为1的标准正态分布。正态分布允许μ取正值和负值,分别表示上升或下降趋势。
参数k从0.5到1.5的均匀分布中获得。均匀分布确保k取值使趋势具有合理和有意义的曲率。
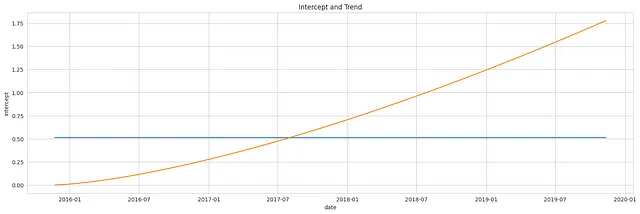
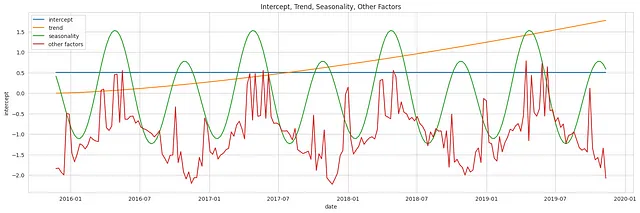
下图展示了从先验分布中获得的单独组件:截距和趋势的样本,分别表示。
季节性
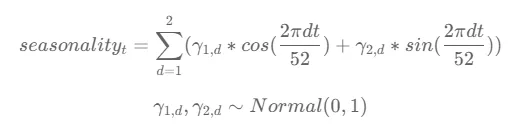
每个组件γ从均值为0,标准差为1的正态分布中获得。
通过将余弦和正弦函数与不同的γ组合,可以建模循环模式,以捕捉数据中存在的季节性。余弦和正弦函数表示在52个单位(周)的周期内观察到的振荡行为。
下图说明了从先验分布中获得的季节性、截距和趋势的样本。

其他因素(控制变量)
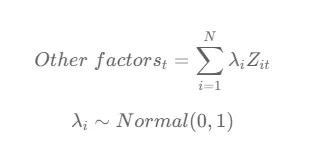
每个因素系数λ从均值为0,标准差为1的正态分布中获得,这意味着λ可以取正值或负值,表示每个因素对结果的影响方向和大小。
下图展示了从先验分布中获得的单独组件:截距、趋势、季节性和控制变量(竞争对手销售B、新闻通讯、假日和活动)各自表示。
媒体渠道
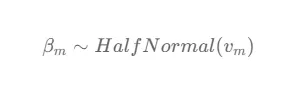
媒体渠道 m 的 β 系数分布被指定为半正态分布,其中标准差参数 v 取决于与媒体渠道 m 相关的总成本之和。总成本反映了分配给特定媒体渠道的投资或资源。
媒体转化

在这些方程中,我们使用一系列转换来建模媒体渠道的行为,例如 adstock 和 Hill 饱和度。
使用 PyMC3 建模市场营销混合
尝试先验、数据规范化和比较贝叶斯建模与 Facebook 的开源 MMM 的 Robyn…
towardsdatascience.com
变量媒体渠道表示时间点 t 上的转换媒体渠道。它通过对原始媒体渠道值 x 进行转换获得。Hill 转换由参数 K(半饱和点,0 0)控制。
变量 x∗ 表示经历 adstock 转换后的时间 t 上的转换媒体渠道值。它是通过将当前原始媒体渠道值与上一个转换值的 adstock 衰减参数 λ 的乘积相加得到的。
参数 K 和 S 遵循形状和比例参数均设置为 1 的伽马分布,而 λ 遵循形状参数为 2,比例参数为 1 的 beta 分布。
Hill 饱和度参数 K 和 S 的概率密度函数如下图所示:
shape = 1scale = 1gamma_dist = stats.gamma(a=shape, scale=scale)samples = gamma_dist.rvs(size=1000)plt.figure(figsize=(20, 6))sns.histplot(samples, bins=50, kde=False, stat='density', alpha=0.5)sns.lineplot(x=np.linspace(0, 6, 100), y=gamma_dist.pdf(np.linspace(0, 6, 100)), color='r')plt.title(f"Gamma Distribution for $K_m$ and $S_m$ with shape={shape} and scale={scale}")plt.xlabel('x')plt.ylabel('P(X=x)')# Show the plotplt.show()python
adstock 参数 λ 的概率密度函数如下图所示:
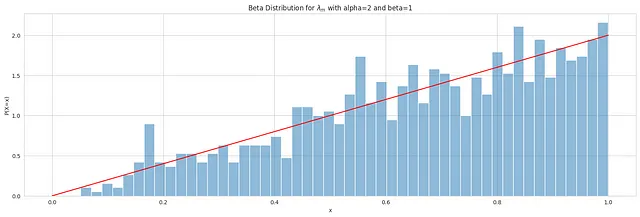
关于 adstock 参数 λ 的规范说明:
Beta(α=2,β=1) 分布的概率密度函数呈现出正趋势,表明更高的值具有更高的概率密度。在媒体分析中,不同的行业和媒体活动可能呈现出不同的衰减速率,大多数媒体渠道通常呈现出较小的衰减率。例如,Robyn 建议常见媒体渠道的 λ 衰减范围如下:电视(0.3–0.8),OOH/印刷/广播(0.1–0.4)和数字媒体(0–0.3)。
在 Beta(α=2,β=1) 分布的上下文中,更接近 1 的 λ 值被赋予更高的概率,而更接近 0 的值被赋予较低的概率。因此,与靠近区间 [0,1] 下限的结果相比,靠近区间上限的结果更有可能发生。
或者,在使用 Carryover 和 Shape Effects 的媒体混合建模的贝叶斯方法中,衰减参数被定义为 Beta(α=3,β=3),其概率密度函数如下图所示。该分布围绕 0.5 对称,表明在区间 [0,1] 的两个极端和中心观测到结果的可能性相等。

下面的图表显示了从先验分布中获取的各个单独组件:截距、趋势、季节性、控制变量和媒体渠道的样本,每个组件都单独表示。

组合所有组件
如前所述,LightweightMMM通过组合来自其先验分布的各种组件,例如截距、趋势、季节性、媒体渠道和其他因素,来模拟加性线性回归,以获得预测响应。下面的图表可视化了真实响应和从先验预测分布中抽样的预期响应。
将单个样本可视化并与真实响应值进行比较,可以观察模型的预测与特定参数值的实际结果相比较的情况。它可以提供对模型在特定实例中的表现的直观理解。
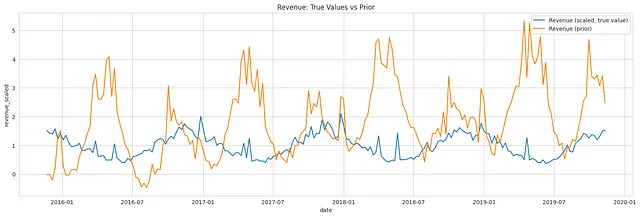
先验预测检查
为了获得更强的洞察力,通常建议从先验预测分布中多次抽样并测量不确定性。先验预测检查有助于评估所选择的模型的适当性,并评估模型的预测是否与我们的期望相一致,在观察任何实际数据之前。
下面所示的图表通过显示每个点的预期收入(平均值)以及不确定性度量来可视化先验预测分布。我们可以看到,真实收入落在标准偏差范围内,表明模型规范适用于观察到的数据。
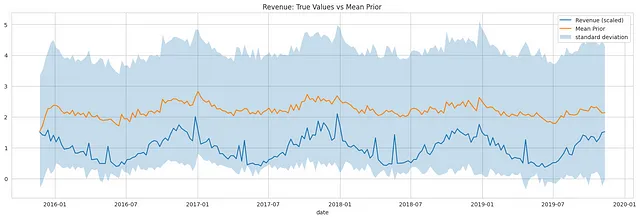
结论
贝叶斯市场混合建模可能需要相当长的时间来掌握。我希望本文有助于增强您对先验分布和贝叶斯营销模型规范的理解。
完整的代码可从我的Github存储库中下载
感谢阅读!