《音频机器学习简介》
Introduction to Audio Machine Learning
我目前正在开发一个音频语音识别系统,所以我需要复习一下关于它的基础知识。这篇文章就是这个目的而写的。
音频介绍
目录
- 介绍
声音 —
- 声音是一个连续信号,有无限的信号值
- 数字设备需要有限的数组,因此我们需要将其转换为一系列离散值
- 又称数字表示
- 声音功率 — 能量传输速率(瓦特)
- 声音强度 — 单位面积的声音功率(瓦特/平方米)
音频文件格式 —
- .wav
- .flac(免费无损音频编解码器)
- .mp3
文件格式通过压缩音频信号的数字表示的方式来区分
转换步骤 —
- 麦克风捕获模拟信号
- 然后将声波转换为电信号
- 然后模拟到数字转换器将这个电信号数字化
采样
- 它是在固定时间步长上测量信号的值的过程
- 一旦采样,采样波形就是离散格式

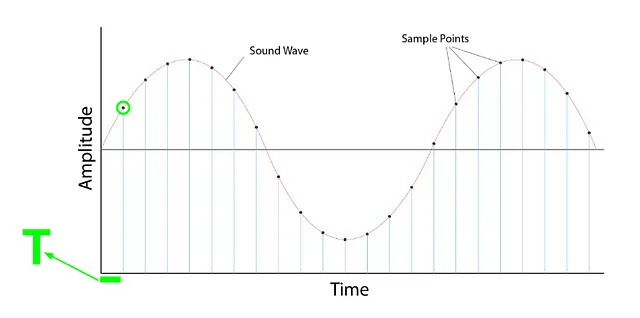
采样率/采样频率
- 每秒采样的样本数
- 例如,如果每秒采样1000个样本,则采样率(SR)= 1000
- 较高的SR -> 更好的音频质量
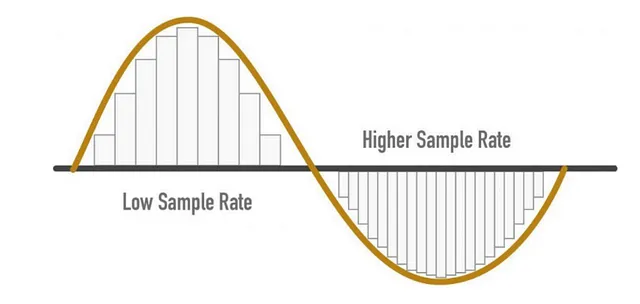
SR注意事项
- 采样率 = (可以从信号中捕获的最高频率)* 2
- 对于人耳-可听频率为8KHz,因此我们可以说采样率(SR)为16KHz
- 尽管更高的SR可以提供更好的音频质量,但并不意味着我们应该不断增加它。
- 在所需的线之后,它不添加任何信息,只增加计算成本
- 此外,较低的SR可能会导致信息丢失
要记住的要点 —
- 在训练时,所有音频样本都应具有相同的采样率
- 如果使用预训练的模型,音频样本应重新采样以与模型训练的音频数据的SR相匹配
- 如果使用来自不同SR的数据,则模型无法很好地泛化
振幅 —
- 声音是由人类可听频率下的气压变化产生的
- 振幅 — 即时的声压级,以分贝(dB)表示
- 振幅是响度的度量
比特深度 —
- 描述了可以描述的精度值的多少
- 比特深度越高,数字表示越接近原始连续声波
- 常见的比特深度值有16位和24位
量化 —
初始时,音频是连续的形式,即平滑的波形。为了将其以数字形式存储,我们需要将其转换为小步长;我们通过量化来实现这一点。
- 本周AI动态,8月7日:生成式AI登陆Jupyter和Stack Overflow • ChatGPT更新
- 5个用于地理空间数据分析的Python包
- 遇见Retroformer:一种优雅的AI框架,通过学习插件回顾模型来迭代改进大型语言代理
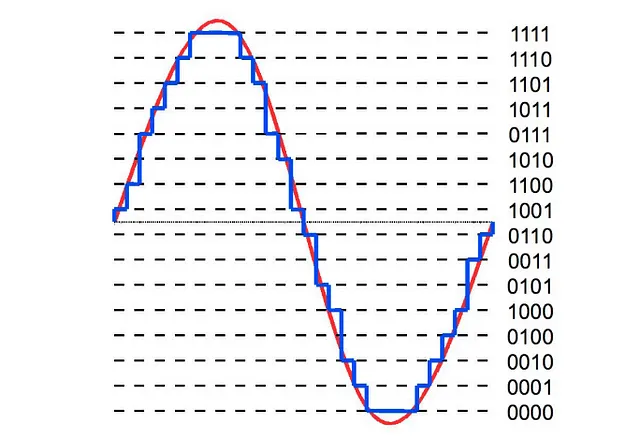
你可以说比特深度是表示音频所需的步数
- 16位音频需要 — 65536个步骤
- 24位音频需要 — 16777216个步骤
- 这种量化引入了噪音,因此更偏好高比特深度
- 尽管这种噪音并不是一个问题
- 16位和24位音频以整数样本存储,而32位音频样本以浮点数存储
- 该模型需要浮点数,因此我们需要在训练模型之前将该音频转换为浮点数
实现 —
#加载库import librosa
#librosa.load函数返回音频数组和采样率audio, sampling_rate = librosa.load(librosa.ex('pistachio'))
import matplotlib.pyplot as pltplt.figure().set_figwidth(12)librosa.display.waveshow(audio,sr = sampling_rate)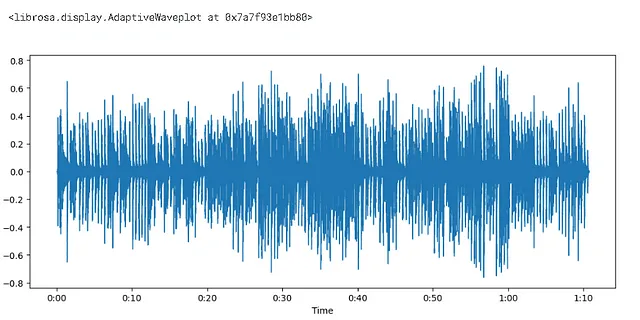
- 振幅在y轴上绘制,时间在x轴上绘制
- 范围从[-1.0,1.0] — 已经是浮点数
print(len(audio))print(sampling_rate/1e3)>>1560384>>22.05
## 频率谱import numpy as np# 而不是关注每个离散值,我们只看前4096个值input_data = audio[:4096]# DFT = 离散傅里叶变换# 使用DFT绘制该频率谱window = np.hanning(len(input_data))window>>array([0.00000000e+00, 5.88561497e-07, 2.35424460e-06, ..., 2.35424460e-06, 5.88561497e-07, 0.00000000e+00])
dft_input = input_data * window
figure = plt.figure(figsize = (15,5))plt.subplot(131)plt.plot(input_data)plt.title('输入')plt.subplot(132)plt.plot(window)plt.title('汉宁窗')plt.subplot(133)plt.plot(dft_input)plt.title('dft_input')# 对每个实例生成类似的绘图
离散频率变换 = DFT
- 如果我说在我们有离散信号数据之前,你会同意吗?
- 如果你同意,那么你可以理解到目前为止,我们的数据在时间域,现在我们想要转换到频率域。这就是为什么DFT先生在这里帮助我们的原因。
# 计算dft - 离散傅里叶变换
dft = np.fft.rfft(dft_input)
plt.plot(dft)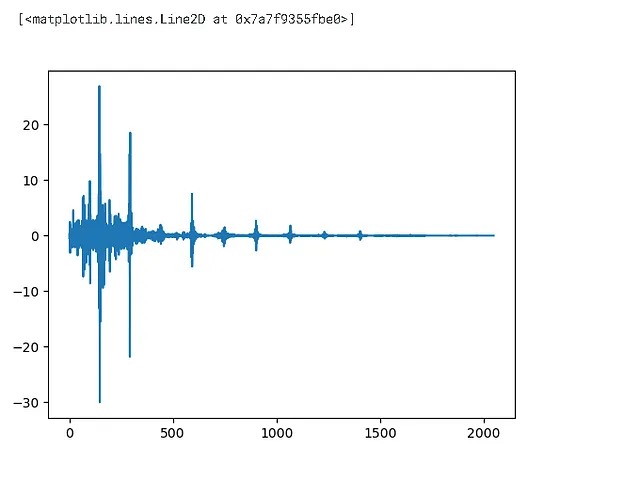
# 幅度
amplitude = np.abs(dft)
# 转换为分贝
amplitude_dB = librosa.amplitude_to_db(amplitude, ref=np.max)
# 有时人们想使用功率谱 -> A**2为什么要取绝对值?
当我们取幅度时,我们应用了abs函数,原因是复数
- 傅里叶变换后的输出以复数形式返回,取绝对值给出了幅度,因此是绝对值。
print(len(amplitude))
print(len(dft_input))
print(len(dft))
>>2049
>>4096
>>2049为什么更新后的数组是原数组的一半加1?
当纯实数输入计算DFT时,输出是厄米对称的,即负频率项只是相应正频率项的复共轭,因此负频率项是多余的。该函数不计算负频率项,因此输出的转换轴的长度为n//2 + 1。[来源-文档]
# 频率
frequency = librosa.fft_frequencies(n_fft=len(input_data), sr=sampling_rate)
plt.figure().set_figwidth(12)
plt.plot(frequency, amplitude_dB)
plt.xlabel("频率(Hz)")
plt.ylabel("幅度(dB)")
plt.xscale("log")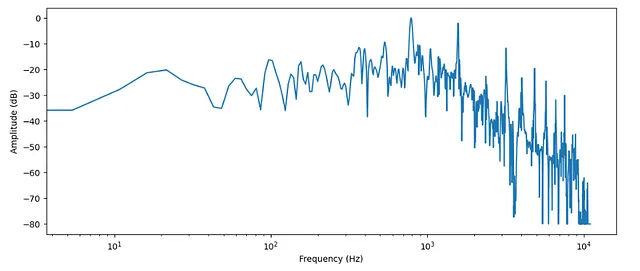
- 如前所述,从时间域到频率域
- 频率域通常用对数刻度表示
谱图 —
- 显示频率随时间变化的方式
- 执行此转换的算法是短时频率变换
如何创建谱图 —
- 谱图是一堆频率变换,如何实现?让我们看看
- 对于给定的音频,我们获取小片段并找到它们的频谱。之后,我们只需将它们沿时间轴堆叠即可。结果图是一个谱图
librosa.stft默认分为2048个片段
频率谱 —
- 表示一刻钟的不同频率的幅度。
- 频率谱对于理解信号在特定时刻的频率成分更加合适。这两种表示都是了解频域信号特性的有价值工具。
- 幅度 vs. 频率
谱图 —
- 通过将信号分成片段并绘制它们的频谱随时间的变化来表示频率内容的变化。
- 谱图特别适用于分析和可视化时变信号,如音频信号或时间序列数据,因为它提供了频率成分在不同时间间隔内如何演变的洞察。
- 频率 vs. 时间
spectogram = librosa.stft(audio)spectogram_to_dB = librosa.amplitude_to_db(np.abs(spectogram),ref = np.max)
plt.figure().set_figwidth(12)librosa.display.specshow(spectogram_to_dB, x_axis="time", y_axis="hz")plt.colorbar()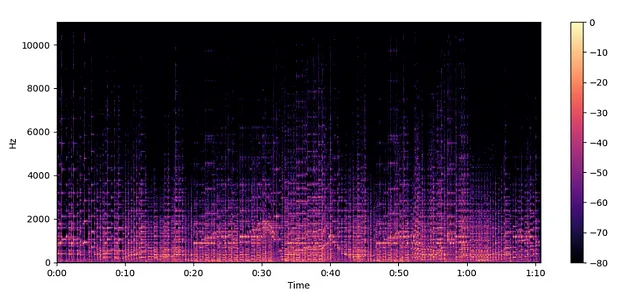
梅尔频谱图 —
- 在不同频率尺度上的频谱图。
在继续之前,必须记住以下几点。
- 在较低频率下,人类对音频的变化更敏感,而在较高频率下则不太敏感
- 这种敏感性随着频率的增加呈对数变化
- 因此,简单来说,梅尔频谱图是频谱图的压缩版本。
MelSpectogram = librosa.feature.melspectrogram(y=audio, sr=sampling_rate, n_mels=128, fmax=8000)MelSpectogram_dB = librosa.power_to_db(MelSpectogram, ref=np.max)plt.figure().set_figwidth(12)librosa.display.specshow(MelSpectogram_dB, x_axis="time", y_axis="mel", sr=sampling_rate, fmax=8000)plt.colorbar()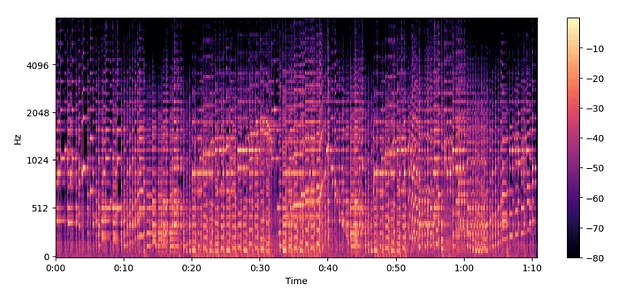
- 上述示例中使用了
librosa.power_to_db(),因为使用了librosa.feature.melspectrogram()来创建功率谱图。
结论 —
梅尔频谱图比普通频谱图捕捉到更有意义的特征,因此更受欢迎。
参考资料 —
Huggingface
个人Kaggle内核(供您练习)
社交媒体 —
Kaggle
如果您喜欢这篇文章,请点赞以示支持。下次见,在下一个笔记本中,我们将看到如何加载和流式传输音频数据。






