本福特定律与机器学习相遇:用于检测假推特关注者的方法
Ford's Law Meets Machine Learning A Method for Detecting Fake Twitter Followers

在广阔的社交媒体数字化领域中,用户的真实性是一个重大关注点。随着Twitter等平台的发展,假账号的增加也在蔓延。这些账号模仿真实用户的活动,在数据中制造噪音,并对数字生态系统的可信度产生负面影响。
传统的检测假账号的方法通常依赖于复杂的机器学习算法。然而,还存在一个有趣的替代工具——Benford定律,这是一种描述许多数字数据集中前导数字频率分布的数学原理。本文探讨如何利用Benford定律的威力,结合机器学习技术,揭示假Twitter粉丝。
Benford定律简介
让我们花一点时间思考在各种数据集中某些数字作为前导数字出现的频率。例如,想象一下你有一个数据集,其中包含你最喜欢的在线市场上的产品价格。你会期望哪个数字最常作为前导数字出现?
直觉上,你可能会认为从1到9的每个数字作为前导数字出现的机会是相等的。毕竟,分布应该是均匀的吧?令人惊讶的是,这种假设是错误的。根据Benford定律,前导数字1出现的频率最高,其次是2、3,依此类推,9是最不常见的。
那么Benford定律到底是什么?
Benford定律也被称为异常数字定律或首位数字定律¹。它提供了在一组自然数字中首位数字d出现的概率。根据该定律,首位数字为1的概率为30.1%,而9的概率则降至4.6%。
如果我问你这个问题:“假设我们有包含2000年美国每个县人口的数据。随机的人口计数以1开头的概率是多少?”你现在知道答案大约是30%:
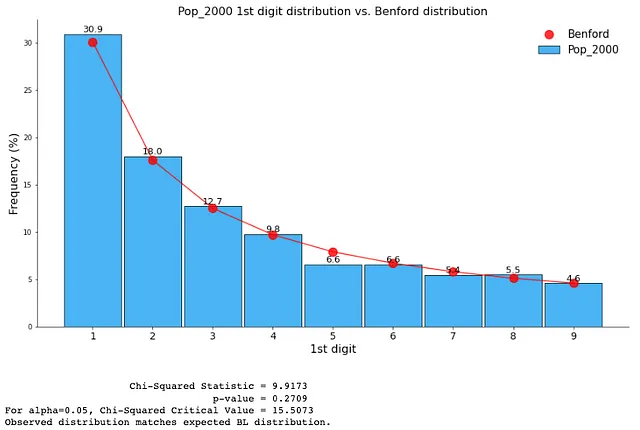
这个有趣的现象挑战了我们传统的期望,并具有深远的影响。它不仅在产品价格和人口数据中观察到,还在各种数据集中出现,如财务报表、股票价格、体育统计数据、Tiktok点赞和科学测量数据。理解和利用Benford定律的威力可以揭示有价值的见解,并增强我们在各个领域中检测异常和异常情况的能力,包括社交媒体分析,如识别假Twitter粉丝。
在本博客中,我深入探讨了Benford定律和机器学习的有趣交叉点,探索了如何将这一数学原理与先进的算法结合起来,揭示并对抗假Twitter粉丝的存在。
数据来源和描述
为了进行这个研究,我使用了一个公开可得的非合成标记的Twitter账户数据集。
Twitter用户数据集的来源是Bot Repository网站²,该网站收集了一系列的Twitter用户账户数据。
在这一步骤中,出现了一个数据限制的问题,因为大部分可用的公共数据都不满足Benford定律所需的至少一个关键假设。因此,我找到的唯一可行的数据集是cresci-2015数据集。
cresci-2015数据集包含了一个由原始作者³手动注释的真实数据和假数据的集合。
在下载了数据集后,我收集并使用了5301个账户(行)和8个特征(列)。虽然数据集包含更多列,但本研究只考虑了以下列与研究相关的内容:
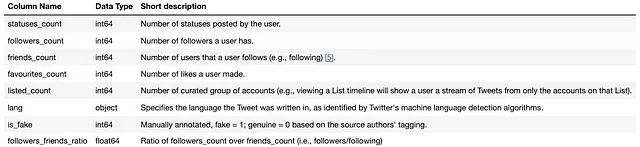
用于简要展示Benford定律的样本的另一个数据集是来自Mark Nigrini的网站⁴的14_Census_2000_2010.csv,他是Benford定律书的作者。
关键假设和示例
在我们深入研究Benford定律的示例和应用之前,让我们回顾一下它的关键假设:
- 数字集合没有限制(所有的首位数字都可能是1到9)
- 数字跨越多个数量级(1-10,10-100,100-1000,至少包含4位数的数字效果最佳)
- 样本大小非常大(如果可能,使用整个人口;样本大小小于1000将产生不可靠的结果)
一些符合或不符合Benford定律(BL)的示例数据集如下⁶:
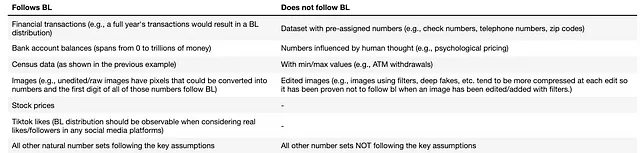
Benford定律在机器学习中的一些主要应用
- 欺诈/异常检测
- 图像取证
- 机器人/假粉丝检测
特征工程
在深入研究机器学习模型之前,我首先创建了一个关注者/好友比例特征,因为假粉丝的社交连接是不自然的。假粉丝的一个关键特征是他们关注的账户比他们的好友(关注)数量少。尽管假粉丝经常试图让其他假粉丝关注他们,但平均而言,他们关注的账户(净好友)的数量仍然显著高于他们的关注者(净关注者)的数量。
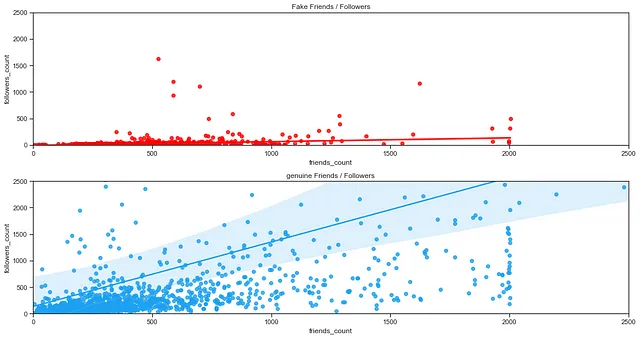
正如上图所示,假账户的关注者数量通常较少,而与之相比,好友的数量较多(回顾一下,这指的是一个账户关注的用户数量 ⁵)。很容易理解为什么假粉丝会关注更多的账户——毕竟,这是他们的主要目的。由于这些假粉丝账户不是为了互动而设计的,它们通常有较低的关注者数量。
检查是否符合Benford定律
基于上述讨论和图表,可以看出机器人或假粉丝建立的社交连接是不自然的,因此它们倾向于违反Benford定律。
在检查Twitter数据集中每个数据子集中的不规则性或假粉丝迹象时,我进行了假设检验:
- 原假设:数据子集遵循Benford定律分布。
- 备择假设:数据子集不遵循Benford定律分布。
我使用了alpha = 0.05的卡方检验来测试我的假设,并确定提出的模型与我们观察到的数据的拟合程度。
将上述测试应用于每个数据子集(仅真实账户、仅假账户和合并数据框)的结果如下:
1. 真实账户上的本福特定律
根据本博客的关键假设和示例部分,只有以下特征可以用来检查本福特定律的符合性:
- followers_count(关注者数)
- statuses_count(状态数)
- favourites_count(收藏数)
如下所示,真实账户遵循本福特分布:
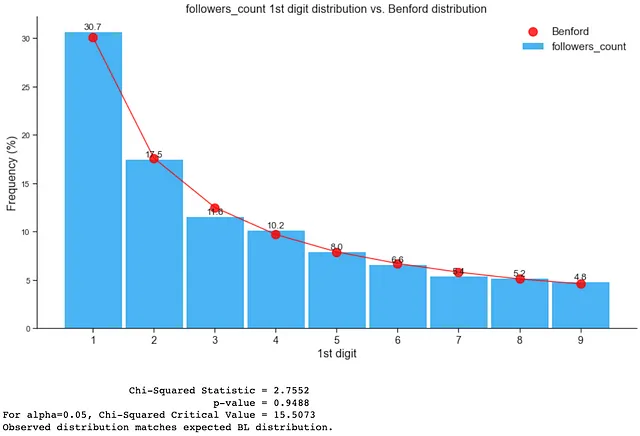


2. 假粉丝账户上的本福特定律
根据本博客的关键假设和示例部分,只有以下特征可以用来检查本福特定律的符合性:
- followers_count(关注者数)
- statuses_count(状态数)
- favourites_count(收藏数)
- friends_count(好友数)
如下所示,仅包含假数据的分布不符合本福特定律:

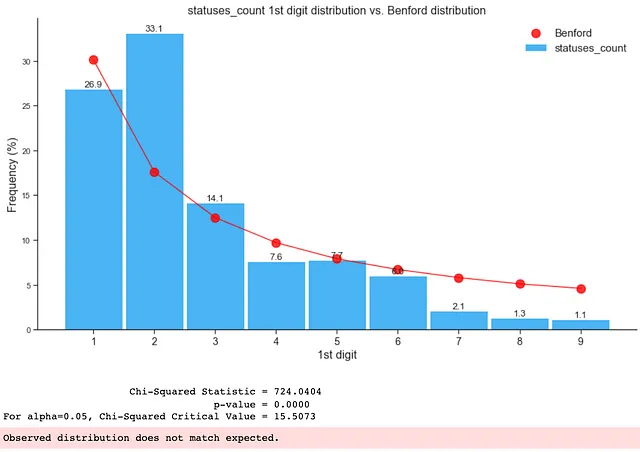
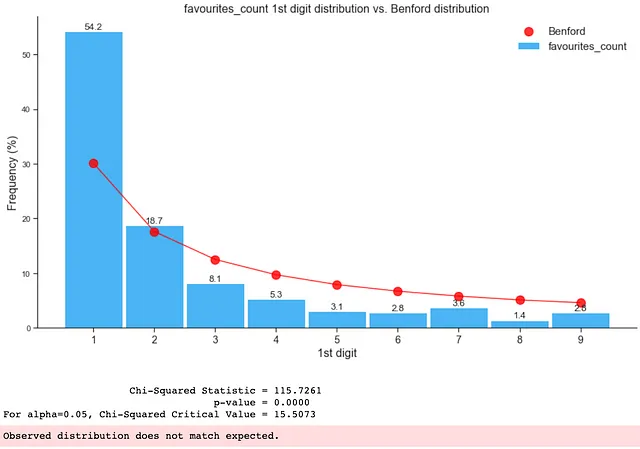

3. 整个数据集(真实和假数据的组合)上的本福特定律
根据本博客的关键假设和示例部分,只有以下特征可以用来检查本福特定律的符合性:
- followers_count(关注者数)
- statuses_count(状态数)
- favourites_count(收藏数)
- friends_count(好友数)
如下所示,整个数据框中存在虚假关注者,导致其不符合本福德分布:
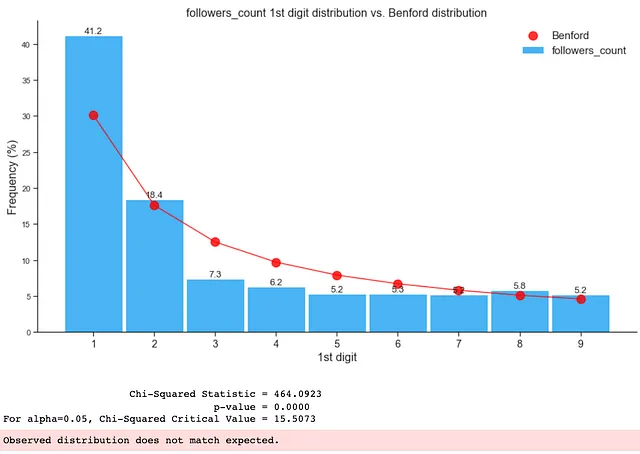
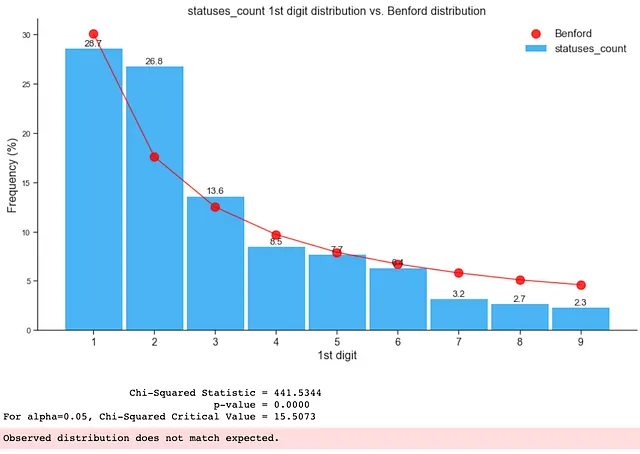
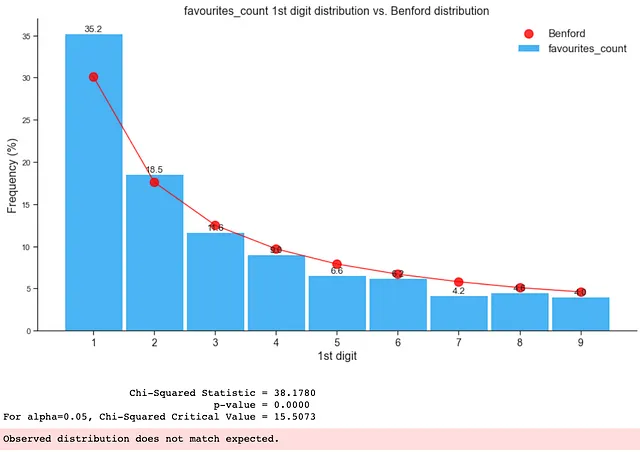
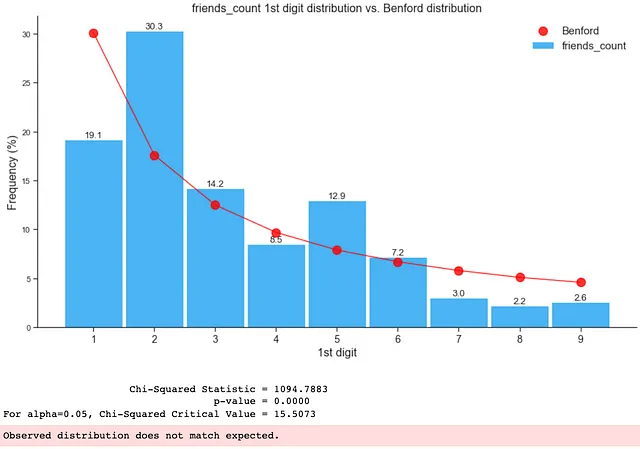
如上所示,通过检查数据集或数据子集的第一位数字分布,我们可以立即看出数据集中是否存在异常或虚假关注者,甚至是机器人。当研究的目标是识别数据集中的异常、操纵或不正常的数字(如欺诈或本研究中的虚假关注者)时,我们可以利用这些见解来确定要优先检查的数据集或子集。
机器学习模型
在本节中,我们将使用机器学习模型来识别Twitter数据集中的虚假关注者。重点是确定由自动机器学习分类器识别出的主要预测变量是否与假账号的社交连接(尤其是关注者与好友比率)存在异常。
为了进行这个分类任务,我使用了一套机器学习模型,包括梯度提升、随机森林和k最近邻(kNN)。通过自动机器学习函数,我确定了用于检测虚假Twitter关注者的顶级预测变量。随后,我将其结果与本福德定律的结果进行比较,以验证结果。
基准:比例性机会准则(PCC)为53%,因此我们必须超过67%的准确率(PCC的1.25倍)。
自动机器学习:执行创建的自动机器学习函数,获取用于检测虚假Twitter关注者的顶级预测变量,并将其结果与BL的结果进行比较:

观察
正如预期的那样,分析显示“关注者/好友比率”始终是最重要的预测变量,与本福德定律的结果一致。这支持了最初的假设,即用户的关注者与好友的比率是确定账号真实性的关键因素。此外,真实关注者作为自然生成的数据集,符合本福德定律。应用本福德定律可以识别数据集中的虚假关注者,因为真实账号遵循本福德定律的分布,而具有虚假关注者的数据集偏离了该定律。
结论
本研究介绍了本福德定律及其在使用cresci-2015数据集的机器学习中的应用。主要挑战是找到一个符合应用本福德定律的前提条件的非合成数据集。关注者数量、好友数量等特征被确定为区分虚假和真实账号的因素。然后,使用这些特征检查它们是否符合本福德定律,并将其应用于机器学习模型来对用户进行分类。模型对于识别虚假关注者的准确率高达99%以上。
虽然虚假关注者试图模仿真实活动,但他们的不自然行为意味着他们违反了本福德定律。即使在他们的首位数字分布中稍微有所变化,也可能导致整个数据偏离本福德定律的分布。
通过应用本福德定律,我们在数据集中检测到了虚假关注者的存在。所有真实账户都符合本福德定律,而包含虚假关注者的数据集(如虚假数据帧和合并/整个数据帧)则不符合。
此外,自动机器学习提供的结果与本福德定律的发现一致。关注者数与好友数的比值是所有使用的机器学习模型中的一项一致的最重要的预测变量。这证实了最初的假设,即用户的关注者与他们的好友(关注对象)的比值是确定账户是否真实或虚假的关键因素。
我们可以得出结论,自然发生的数据集符合本福德定律。本福德定律的简单可视化既可以作为检测异常的流程的一部分,也可以作为探索性数据分析的一部分,用于识别数据集中的潜在错误、欺诈、操纵偏差或处理效率问题。此外,本福德定律还可以作为存在虚假关注者的初步指标,提供一个粗略但有价值的初步识别工具。最后,对于大型数据集,本福德定律可以帮助在开始机器学习建模过程之前,对子集中的偏差进行高度专注的测试。
未来研究建议
由于本研究的主要目的是介绍本福德定律如何作为补充或帮助提供关于数据集中任何异常或操纵迹象的简单和即时洞察力,因此有许多改进可以在未来的研究中实施。根据我们的分析和结论的洞察,以下项目强烈建议用于未来的研究:
- 使用更大的数据集:为了充分展示本福德定律作为ML流程的补充或一部分甚至作为EDA的优点和用途,因为本福德定律的结果在数据集大小增加时往往更准确,最好使用更大的数据集。
- 实时虚假关注者检测:考虑到本博客中讨论的结果,将本福德定律和机器学习虚假关注者检测工作实时化,作为Web或应用程序附加组件,以帮助用户立即检测应用程序中存在的虚假关注者或甚至机器人。
- 考虑其他非数字特征以构建更强大的模型:使用自然语言处理或信息检索和其他模型处理和包含用户实际发表的非数字特征,可以与前述的本福德定律和ML步骤结合使用,以增强数据集的精确度和召回率。
进一步探索和研究本福德定律与改进机器学习模型以检测虚假关注者有关的内容,将有助于使Twitter和其他社交媒体应用成为对所有真实用户而言更安全的环境。
源代码
如果您想探索此项目的更全面的分析和代码,请随时点击此链接访问我的GitHub存储库。谢谢!
参考资料
[1] Benford, F. (1938). The Law of Anomalous Numbers. Proceedings of the American Philosophical Society, 78(4), 551–572. https://www.jstor.org/stable/984802
[2] Bot Repository developers. (2022, November). Bot Repository Website. https://botometer.osome.iu.edu/bot-repository/datasets.html .
[3] Cresci, S., Di Pietro, R., Petrocchi, M., Spognardi, A., & Tesconi, M. (2015). Fame for sale: efficient detection of fake Twitter followers. arXiv:1509.04098 09/2015. Elsevier Decision Support Systems, Volume 80, December 2015, Pages 56–71.
[4] Nigrini, M. (Wiley, 2012). Benford’s Law. https://nigrini.com/benfords-law/
[5] Twitter Developers. (2022, November). Follow, search, and get users. https://developer.twitter.com/en/docs/twitter-api/v1/accounts-and-users/follow-search-get-users/overview
[6] National Association of State Auditors, Comptrollers and Treasurers. (2017). Fraud Analysis and Detection: Using Benfords Law and Other Effective Techniques. https://www.youtube.com/watch?v=9tpGVq5DcTw&t=4961s





