是的,变压器在时间序列预测中非常有效(+自动形式转换器)
Yes, transformers are very effective in time series forecasting (+ automatic format conversion).
介绍
几个月前,我们介绍了 Inforer 模型(周浩一等人,2021年),这是一个时间序列 Transformer 模型,获得了AAAI 2021最佳论文奖。我们还提供了一个使用 Inforer 进行多元概率预测的示例。在这篇文章中,我们讨论了一个问题:Transformer 模型对时间序列预测是否有效?(AAAI 2023)。正如我们将看到的,它们确实有效。
首先,我们将提供实证证据,证明Transformer 模型对时间序列预测确实有效。我们的比较表明,简单的线性模型DLinear并不比Transformer模型更好,正如其声称的那样。当与相同设置中的等效大小的线性模型进行比较时,基于Transformer的模型在我们考虑的测试集度量指标上表现更好。然后,我们将介绍Autoformer模型(吴海旭等人,2021年),该模型是在Informer模型之后于NeurIPS 2021发表的。Autoformer模型现在可以在🤗 Transformers中使用。最后,我们将讨论DLinear模型,这是一个简单的前馈网络,使用了Autoformer的分解层。DLinear模型最初是在”Are Transformers Effective for Time Series Forecasting?”中介绍的,并声称在时间序列预测中优于基于Transformer的模型。
让我们开始吧!
基准测试- Transformers vs. DLinear
在最近发表的AAAI 2023年论文”Are Transformers Effective for Time Series Forecasting?”中,作者声称Transformer模型对时间序列预测无效。他们将基于Transformer的模型与一个简单的线性模型(称为DLinear)进行了比较。DLinear模型使用了Autoformer模型的分解层,我们将在本文后面介绍。作者声称DLinear模型在时间序列预测中优于基于Transformer的模型。那真的是这样吗?让我们来看一下。
上表显示了在论文中使用的三个数据集上Autoformer模型与DLinear模型之间的比较结果。结果表明,Autoformer模型在这三个数据集上优于DLinear模型。
接下来,我们将介绍新的Autoformer模型和DLinear模型。我们将展示如何在上表的Traffic数据集上对它们进行比较,并解释我们得到的结果。
TL;DR:简单的线性模型在某些情况下具有优势,但在单变量情况下,与Transformer等复杂模型相比,它无法纳入协变量。
Autoformer – Under The Hood
Autoformer建立在传统的时间序列分解为季节性和趋势-周期成分的方法之上。这通过引入一个分解层来实现,该层增强了模型准确捕捉这些成分的能力。此外,Autoformer引入了一种创新的自相关机制,用于替代传统Transformer中的自注意力机制。这种机制使模型能够利用基于周期的依赖关系,从而提高整体性能。
在接下来的章节中,我们将深入探讨Autoformer的两个关键贡献:分解层和注意力(自相关)机制。我们还将提供代码示例,以说明这些组件在Autoformer架构中的功能。
分解层
分解一直是时间序列分析中的一种常用方法,但在Autoformer论文的引入之前,它在深度学习模型中并没有被广泛应用。在简要解释了该概念之后,我们将演示如何在Autoformer中应用这一思想,使用PyTorch代码。
时间序列的分解
在时间序列分析中,分解是一种将时间序列分解为三个系统成分的方法:趋势-周期、季节性变化和随机波动。趋势成分代表时间序列的长期趋势,可以是递增、递减或稳定的。季节性成分代表时间序列中发生的周期性模式,例如年度或季度周期。最后,随机(有时称为“不规则”)成分代表数据中无法用趋势或季节性成分解释的随机噪声。
分解的两种主要类型是加法分解和乘法分解,这在很棒的 statsmodels 库中实现。通过将时间序列分解为这些成分,我们可以更好地理解和建模数据中的潜在模式。
但是我们如何将分解结合到Transformer架构中呢?让我们看看Autoformer是如何做到的。
Autoformer中的分解
Autoformer将分解块作为模型的内部操作,如上图所示。可以看到,编码器和解码器使用分解块逐步聚合趋势-周期部分,并从序列中提取季节性部分。自从Autoformer发表以来,内部分解的概念已经证明了其有用性。随后,它被应用于其他一些时间序列论文中,如FEDformer(周、天等,ICML 2022)和DLinear(曾、艾玲等,AAAI 2023),突显了它在时间序列建模中的重要性。
现在,让我们正式定义分解层:
对于长度为 L L L 的输入序列 X ∈ R L × d \mathcal{X} \in \mathbb{R}^{L \times d} X ∈ R L × d ,分解层返回定义的 X trend , X seasonal \mathcal{X}_\textrm{trend}, \mathcal{X}_\textrm{seasonal} X trend , X seasonal :
X trend = AvgPool(Padding( X )) X seasonal = X − X trend \mathcal{X}_\textrm{trend} = \textrm{AvgPool(Padding(} \mathcal{X} \textrm{))} \\ \mathcal{X}_\textrm{seasonal} = \mathcal{X} – \mathcal{X}_\textrm{trend} X trend = AvgPool(Padding( X )) X seasonal = X − X trend
PyTorch中的实现:
import torch
from torch import nn
class DecompositionLayer(nn.Module):
"""
返回时间序列的趋势和季节性部分。
"""
def __init__(self, kernel_size):
super().__init__()
self.kernel_size = kernel_size
self.avg = nn.AvgPool1d(kernel_size=kernel_size, stride=1, padding=0) # 移动平均
def forward(self, x):
"""输入形状:Batch x Time x EMBED_DIM"""
# 在时间序列的两端进行填充
num_of_pads = (self.kernel_size - 1) // 2
front = x[:, 0:1, :].repeat(1, num_of_pads, 1)
end = x[:, -1:, :].repeat(1, num_of_pads, 1)
x_padded = torch.cat([front, x, end], dim=1)
# 计算系列的趋势和季节性部分
x_trend = self.avg(x_padded.permute(0, 2, 1)).permute(0, 2, 1)
x_seasonal = x - x_trend
return x_seasonal, x_trend如您所见,实现非常简单,可以在其他模型中使用,正如我们将在DLinear中看到的那样。现在,让我们解释第二个贡献 – 注意力(自相关)机制。
注意力(自相关)机制
除了分解层外,Autoformer还采用了一种新颖的自相关机制,它无缝地取代了自注意力。在传统的时间序列Transformer中,注意力权重是在时间域中计算的,并进行逐点聚合。另一方面,如上图所示,Autoformer在频率域中计算它们(使用快速傅里叶变换)并通过时间延迟进行聚合。
在接下来的章节中,我们将详细介绍这些主题,并通过代码示例进行解释。
频率域注意力
理论上,给定时间滞后 τ \tau τ ,自相关用于衡量单个离散变量 y y y 的“关系”(皮尔逊相关性),该关系衡量变量在时间 t t t 的当前值与时间 t − τ t-\tau t − τ 的过去值之间的关联:
自相关( τ )= Corr ( y t , y t − τ ) \textrm{自相关}(\tau) = \textrm{Corr}(y_t, y_{t-\tau}) 自相关( τ )= Corr ( y t , y t − τ )
使用自相关,Autoformer从查询和键中提取基于频率的依赖关系,而不是它们之间的标准点积。您可以将其视为自注意力中的QKT替代项。
在实践中,通过FFT一次性计算查询和键的所有滞后的自相关。通过这样做,自相关机制实现了O(LlogL)的时间复杂度(其中L是输入时间长度),类似于Informer的ProbSparse attention。请注意,使用FFT计算自相关的理论基于维纳-辛钦定理,超出了本博文的范围。
现在,我们准备看一下PyTorch中的代码:
import torch
def autocorrelation(query_states, key_states):
"""
使用`torch.fft`计算自相关(Q,K)。
将其视为自注意力中QK^T的替代项。
假设状态已调整为相同的形状[batch_size, time_length, embedding_dim]。
"""
query_states_fft = torch.fft.rfft(query_states, dim=1)
key_states_fft = torch.fft.rfft(key_states, dim=1)
attn_weights = query_states_fft * torch.conj(key_states_fft)
attn_weights = torch.fft.irfft(attn_weights, dim=1)
return attn_weights非常简单! 😎 请注意,这只是autocorrelation(Q,K)的部分实现,完整实现可在🤗 Transformers中找到。
接下来,我们将看到如何通过时间延迟来聚合我们的attn_weights和值,这个过程被称为时间延迟聚合。
时间延迟聚合
让我们将自相关(称为attn_weights)记为R(Q,K)。问题是:我们如何聚合这些R(Q,K)(τ1), R(Q,K)(τ2), …, R(Q,K)(τk)与V?在标准的自注意力机制中,这种聚合是通过点积完成的。然而,在Autoformer中,我们采用了一种不同的方法。首先,我们通过计算每个时间延迟τ1, τ2, …, τk的V的值来对齐V,这也被称为Rolling。然后,我们对齐的V和自相关进行逐元素乘法。在提供的图中,您可以看到左侧展示了V通过时间延迟的滚动,而右侧则说明了与自相关的逐元素乘法。
可以用以下方程总结:
τ1, τ2, …, τk = arg Top-k(R(Q,K)(τ))
R̂Q,K(τ1), R̂Q,K(τ2), …, R̂Q,K(τk) = Softmax(R(Q,K)(τ1), R(Q,K)(τ2), …, R(Q,K)(τk))
自相关-注意力 = ∑i=1^k Roll(V, τi) ⋅ R̂Q,K(τi)
就是这样!请注意,k k k由一个称为autocorrelation_factor的超参数控制(类似于Informer中的sampling_factor),并且在乘法之前对自相关性应用softmax。
现在,我们准备看最终的代码:
import torch
import math
def time_delay_aggregation(attn_weights, value_states, autocorrelation_factor=2):
"""
计算聚合作为value_states.roll(delay) * top_k_autocorrelations(delay)。
最终结果是自相关-注意力的输出。
将其视为attn_weights和value states之间的点积的替代。
自相关因子用于找到前k个自相关延迟。
假设:value_states和attn_weights形状:[batch_size, time_length, embedding_dim]
"""
bsz, num_heads, tgt_len, channel = ...
time_length = value_states.size(1)
autocorrelations = attn_weights.view(bsz, num_heads, tgt_len, channel)
# 找到前k个自相关延迟
top_k = int(autocorrelation_factor * math.log(time_length))
autocorrelations_mean = torch.mean(autocorrelations, dim=(1, -1)) # bsz x tgt_len
top_k_autocorrelations, top_k_delays = torch.topk(autocorrelations_mean, top_k, dim=1)
# 在通道维度上应用softmax
top_k_autocorrelations = torch.softmax(top_k_autocorrelations, dim=-1) # bsz x top_k
# 计算聚合:value_states.roll(delay) * top_k_autocorrelations(delay)
delays_agg = torch.zeros_like(value_states).float() # bsz x time_length x channel
for i in range(top_k):
value_states_roll_delay = value_states.roll(shifts=-int(top_k_delays[i]), dims=1)
top_k_at_delay = top_k_autocorrelations[:, i]
# 聚合
top_k_resized = top_k_at_delay.view(-1, 1, 1).repeat(num_heads, tgt_len, channel)
delays_agg += value_states_roll_delay * top_k_resized
attn_output = delays_agg.contiguous()
return attn_output<p我们成功了!Autoformer模型现在可以在🤗 Transformers库中使用,并简单地称为AutoformerModel。
我们的策略是展示单变量Transformer模型在性能上与本质上是单变量的DLinear模型的比较。我们还将展示在相同数据上训练的两个多变量Transformer模型的结果。
DLinear-揭秘
<p实际上,DLinear的概念很简单:它只是一个具有Autoformer的DecompositionLayer的全连接层。它使用上面的DecompositionLayer将输入的时间序列分解为残差(季节性)和趋势部分。在前向传递中,每个部分都通过自己的线性层,将信号投影到适当大小的prediction_length输出。最终输出是点预测模型中两个相应输出的总和:
def forward(self, context):
seasonal, trend = self.decomposition(context)
seasonal_output = self.linear_seasonal(seasonal)
trend_output = self.linear_trend(trend)
return seasonal_output + trend_output<p在概率设置中,可以通过linear_seasonal和linear_trend层将上下文长度数组投影到prediction_length * hidden维度。将结果输出相加并重塑为(prediction_length, hidden)。最后,概率头将大小为hidden的潜在表示映射到某个分布的参数。
<p在我们的基准测试中,我们使用了GluonTS中的DLinear实现。
示例:交通数据集
<p我们想通过在traffic数据集上进行基准测试来从实证上展示库中基于Transformer的模型的性能。该数据集包含862个时间序列。我们将在每个单独的时间序列上训练一个共享模型(即单变量设置)。每个时间序列表示传感器的占用值,并且在范围[0, 1]内。我们将为所有模型保持以下超参数不变:
# 交通预测长度为24。参考链接:
# https://github.com/awslabs/gluonts/blob/6605ab1278b6bf92d5e47343efcf0d22bc50b2ec/src/gluonts/dataset/repository/_lstnet.py#L105
预测长度 = 24
上下文长度 = 预测长度 * 2
批大小 = 128
每个时期批次数 = 100
时期数 = 50
缩放 = "std"transformers模型都相对较小,具体如下:
编码器层数=2
解码器层数=2
模型维度=16不需要展示如何使用Autoformer训练模型,可以直接将前两篇博客中的模型(TimeSeriesTransformer和Informer)替换为新的Autoformer模型,并在traffic数据集上进行训练。为了不重复劳动,我们已经训练并将模型推送到HuggingFace Hub。我们将使用这些模型进行评估。
加载数据集
首先安装必要的库:
!pip install -q transformers datasets evaluate accelerate "gluonts[torch]" ujson tqdmtraffic数据集在Lai等人(2017)中使用,包含了旧金山交通数据。数据集包含862个小时级时间序列,显示了2015年至2016年旧金山湾区高速公路上的道路占用率,范围为[0, 1]。
from gluonts.dataset.repository.datasets import get_dataset
数据集 = get_dataset("traffic")
频率 = 数据集.metadata.freq
预测长度 = 数据集.metadata.prediction_length让我们可视化数据集中的一个时间序列,并绘制训练集/测试集划分:
import matplotlib.pyplot as plt
训练示例 = next(iter(数据集.train))
测试示例 = next(iter(数据集.test))
样本数 = 4 * 预测长度
图, 轴 = plt.subplots()
轴.plot(训练示例["target"][-样本数:], color="blue")
轴.plot(
测试示例["target"][-样本数 - 预测长度:],
color="red",
alpha=0.5,
)
plt.show()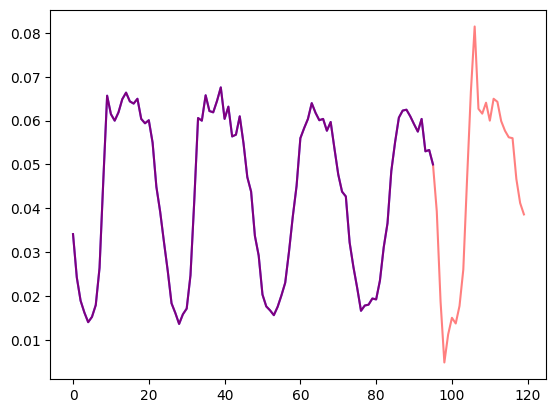
让我们定义训练集/测试集划分:
训练数据集 = 数据集.train
测试数据集 = 数据集.test定义转换
接下来,我们为数据定义转换,特别是用于创建时间特征的转换(基于数据集或通用的特征)。
我们使用GluonTS定义一个转换的链(类似于图像中的torchvision.transforms.Compose),它允许我们将多个转换组合成单个管道。
下面的转换带有注释,以解释它们的作用。在高层次上,我们将遍历数据集的每个时间序列,并添加/删除字段或特征:
from transformers import PretrainedConfig
from gluonts.time_feature import time_features_from_frequency_str
from gluonts.dataset.field_names import FieldName
from gluonts.transform import (
AddAgeFeature,
AddObservedValuesIndicator,
AddTimeFeatures,
AsNumpyArray,
Chain,
ExpectedNumInstanceSampler,
RemoveFields,
SelectFields,
SetField,
TestSplitSampler,
Transformation,
ValidationSplitSampler,
VstackFeatures,
RenameFields,
)
def create_transformation(freq: str, config: PretrainedConfig) -> Transformation:
# 创建一个待删除的字段列表
待删除字段 = []
if config.num_static_real_features == 0:
待删除字段.append(FieldName.FEAT_STATIC_REAL)
if config.num_dynamic_real_features == 0:
待删除字段.append(FieldName.FEAT_DYNAMIC_REAL)
if config.num_static_categorical_features == 0:
待删除字段.append(FieldName.FEAT_STATIC_CAT)
return Chain(
# 步骤1:如果未指定,则删除静态/动态字段
[RemoveFields(field_names=待删除字段)]
# 步骤2:将数据转换为NumPy数组(可能不需要)
+ (
[
AsNumpyArray(
field=FieldName.FEAT_STATIC_CAT,
expected_ndim=1,
dtype=int,
)
]
if config.num_static_categorical_features > 0
else []
)
+ (
[
AsNumpyArray(
field=FieldName.FEAT_STATIC_REAL,
expected_ndim=1,
)
]
if config.num_static_real_features > 0
else []
)
+ [
AsNumpyArray(
field=FieldName.TARGET,
# 对于多变量情况,我们期望额外的维度:
expected_ndim=1 if config.input_size == 1 else 2,
),
# 步骤3:通过零填充目标值来处理NaN,并返回掩码(观测到的值为True,NaN为False)
# 解码器使用这个掩码(未观测到的值不会产生损失)
# 参见xxxForPrediction模型中的loss_weights
AddObservedValuesIndicator(
target_field=FieldName.TARGET,
output_field=FieldName.OBSERVED_VALUES,
),
# 步骤4:根据数据集的频率添加时间特征,作为位置编码
AddTimeFeatures(
start_field=FieldName.START,
target_field=FieldName.TARGET,
output_field=FieldName.FEAT_TIME,
time_features=time_features_from_frequency_str(freq),
pred_length=config.prediction_length,
),
# 步骤5:添加另一个时间特征(仅一个数字)
# 告诉模型时间序列的值在生命周期中的位置
# 类似于运行计数器
AddAgeFeature(
target_field=FieldName.TARGET,
output_field=FieldName.FEAT_AGE,
pred_length=config.prediction_length,
log_scale=True,
),
# 步骤6:将所有时间特征垂直堆叠到键FEAT_TIME中
VstackFeatures(
output_field=FieldName.FEAT_TIME,
input_fields=[FieldName.FEAT_TIME, FieldName.FEAT_AGE]
+ (
[FieldName.FEAT_DYNAMIC_REAL]
if config.num_dynamic_real_features > 0
else []
),
),
# 步骤7:重命名以匹配HuggingFace的命名
RenameFields(
mapping={
FieldName.FEAT_STATIC_CAT: "static_categorical_features",
FieldName.FEAT_STATIC_REAL: "static_real_features",
FieldName.FEAT_TIME: "time_features",
FieldName.TARGET: "values",
FieldName.OBSERVED_VALUES: "observed_mask",
}
),
]
)定义InstanceSplitter
为了进行训练/验证/测试,我们接下来创建一个InstanceSplitter,用于从数据集中抽样窗口(因为由于时间和内存限制,我们不能将整个值的历史传递给模型)。
实例拆分器从数据中随机抽样大小为context_length的窗口,并在后续的prediction_length大小的窗口中添加past_或future_键到相应窗口的时间键中。这确保了values将被拆分为past_values和后续的future_values键,分别用作编码器和解码器的输入。对于time_series_fields参数中的任何键也是如此:
from gluonts.transform import InstanceSplitter
from gluonts.transform.sampler import InstanceSampler
from typing import Optional
def create_instance_splitter(
config: PretrainedConfig,
mode: str,
train_sampler: Optional[InstanceSampler] = None,
validation_sampler: Optional[InstanceSampler] = None,
) -> Transformation:
assert mode in ["train", "validation", "test"]
instance_sampler = {
"train": train_sampler
or ExpectedNumInstanceSampler(
num_instances=1.0, min_future=config.prediction_length
),
"validation": validation_sampler
or ValidationSplitSampler(min_future=config.prediction_length),
"test": TestSplitSampler(),
}[mode]
return InstanceSplitter(
target_field="values",
is_pad_field=FieldName.IS_PAD,
start_field=FieldName.START,
forecast_start_field=FieldName.FORECAST_START,
instance_sampler=instance_sampler,
past_length=config.context_length + max(config.lags_sequence),
future_length=config.prediction_length,
time_series_fields=["time_features", "observed_mask"],
)创建PyTorch DataLoaders
接下来,是时候创建PyTorch DataLoaders了,这使我们能够获得(输入,输出)对的批次 – 或者换句话说(past_values,future_values)。
from typing import Iterable
import torch
from gluonts.itertools import Cyclic, Cached
from gluonts.dataset.loader import as_stacked_batches
def create_train_dataloader(
config: PretrainedConfig,
freq,
data,
batch_size: int,
num_batches_per_epoch: int,
shuffle_buffer_length: Optional[int] = None,
cache_data: bool = True,
**kwargs,
) -> Iterable:
PREDICTION_INPUT_NAMES = [
"past_time_features",
"past_values",
"past_observed_mask",
"future_time_features",
]
if config.num_static_categorical_features > 0:
PREDICTION_INPUT_NAMES.append("static_categorical_features")
if config.num_static_real_features > 0:
PREDICTION_INPUT_NAMES.append("static_real_features")
TRAINING_INPUT_NAMES = PREDICTION_INPUT_NAMES + [
"future_values",
"future_observed_mask",
]
transformation = create_transformation(freq, config)
transformed_data = transformation.apply(data, is_train=True)
if cache_data:
transformed_data = Cached(transformed_data)
# 我们初始化一个Training实例
instance_splitter = create_instance_splitter(config, "train")
# 实例拆分器将从可能的366个转换时间序列中随机抽样长度为上下文长度+滞后长度+预测长度的窗口
# 从目标时间序列内部,并返回一个迭代器。
stream = Cyclic(transformed_data).stream()
training_instances = instance_splitter.apply(stream, is_train=True)
return as_stacked_batches(
training_instances,
batch_size=batch_size,
shuffle_buffer_length=shuffle_buffer_length,
field_names=TRAINING_INPUT_NAMES,
output_type=torch.tensor,
num_batches_per_epoch=num_batches_per_epoch,
)
def create_test_dataloader(
config: PretrainedConfig,
freq,
data,
batch_size: int,
**kwargs,
):
PREDICTION_INPUT_NAMES = [
"past_time_features",
"past_values",
"past_observed_mask",
"future_time_features",
]
if config.num_static_categorical_features > 0:
PREDICTION_INPUT_NAMES.append("static_categorical_features")
if config.num_static_real_features > 0:
PREDICTION_INPUT_NAMES.append("static_real_features")
transformation = create_transformation(freq, config)
transformed_data = transformation.apply(data, is_train=False)
# 我们创建一个测试实例拆分器,它将仅为编码器采样在训练期间看到的最后一个上下文窗口。
instance_sampler = create_instance_splitter(config, "test")
# 我们在测试模式下应用转换
testing_instances = instance_sampler.apply(transformed_data, is_train=False)
return as_stacked_batches(
testing_instances,
batch_size=batch_size,
output_type=torch.tensor,
field_names=PREDICTION_INPUT_NAMES,
)在Autoformer上进行评估
我们已经在这个数据集上预训练了一个Autoformer模型,所以我们可以直接获取模型并在测试集上进行评估:
from transformers import AutoformerConfig, AutoformerForPrediction
config = AutoformerConfig.from_pretrained("kashif/autoformer-traffic-hourly")
model = AutoformerForPrediction.from_pretrained("kashif/autoformer-traffic-hourly")
test_dataloader = create_test_dataloader(
config=config,
freq=freq,
data=test_dataset,
batch_size=64,
)在推断时,我们将使用模型的generate()方法,从训练集中每个时间序列的最后一个上下文窗口预测prediction_length步的未来。
from accelerate import Accelerator
accelerator = Accelerator()
device = accelerator.device
model.to(device)
model.eval()
forecasts_ = []
for batch in test_dataloader:
outputs = model.generate(
static_categorical_features=batch["static_categorical_features"].to(device)
if config.num_static_categorical_features > 0
else None,
static_real_features=batch["static_real_features"].to(device)
if config.num_static_real_features > 0
else None,
past_time_features=batch["past_time_features"].to(device),
past_values=batch["past_values"].to(device),
future_time_features=batch["future_time_features"].to(device),
past_observed_mask=batch["past_observed_mask"].to(device),
)
forecasts_.append(outputs.sequences.cpu().numpy())模型输出的张量形状为(batch_size,样本数量,预测长度,输入大小)。
在这种情况下,我们得到每个测试数据加载器批次中每个时间序列的下一个24小时的100个可能值,回想一下,批次大小是64:
forecasts_[0].shape
>>> (64, 100, 24)我们将它们垂直堆叠起来,以获取测试数据集中所有时间序列的预测结果:测试集中有7个滚动窗口,这就是为什么我们最终得到了7 * 862 = 6034个预测结果:
import numpy as np
forecasts = np.vstack(forecasts_)
print(forecasts.shape)
>>> (6034, 100, 24)我们可以使用🤗 Evaluate库评估与测试集中的真实值比较的预测结果。为此,我们将使用MASE指标。
我们计算数据集中每个时间序列的指标,并返回平均值:
from tqdm.autonotebook import tqdm
from evaluate import load
from gluonts.time_feature import get_seasonality
mase_metric = load("evaluate-metric/mase")
forecast_median = np.median(forecasts, 1)
mase_metrics = []
for item_id, ts in enumerate(tqdm(test_dataset)):
training_data = ts["target"][:-prediction_length]
ground_truth = ts["target"][-prediction_length:]
mase = mase_metric.compute(
predictions=forecast_median[item_id],
references=np.array(ground_truth),
training=np.array(training_data),
periodicity=get_seasonality(freq))
mase_metrics.append(mase["mase"])因此,Autoformer模型的结果是:
print(f"Autoformer单变量MASE:{np.mean(mase_metrics):.3f}")
>>> Autoformer单变量MASE:0.910要绘制任何时间序列与与地面真实测试数据的预测结果,我们定义以下辅助函数:
import matplotlib.dates as mdates
import pandas as pd
test_ds = list(test_dataset)
def plot(ts_index):
fig, ax = plt.subplots()
index = pd.period_range(
start=test_ds[ts_index][FieldName.START],
periods=len(test_ds[ts_index][FieldName.TARGET]),
freq=test_ds[ts_index][FieldName.START].freq,
).to_timestamp()
ax.plot(
index[-5*prediction_length:],
test_ds[ts_index]["target"][-5*prediction_length:],
label="实际",
)
plt.plot(
index[-prediction_length:],
np.median(forecasts[ts_index], axis=0),
label="中位数",
)
plt.gcf().autofmt_xdate()
plt.legend(loc="best")
plt.show()例如,对于测试集中索引为4的时间序列:
plot(4)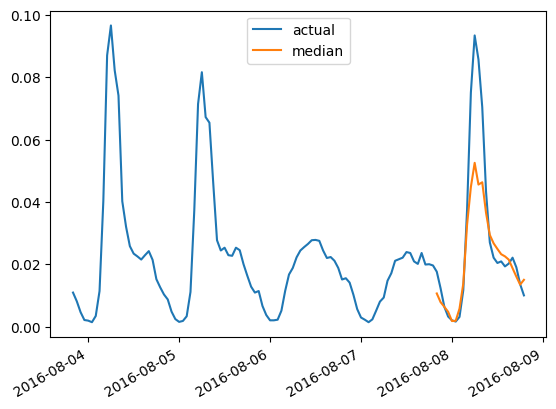
在DLinear上进行评估
我们在gluonts中实现了一个概率DLinear模型,因此我们可以在这里进行快速训练和评估:
from gluonts.torch.model.d_linear.estimator import DLinearEstimator
# 使用与Autoformer模型相同的参数定义DLinear模型
estimator = DLinearEstimator(
prediction_length=dataset.metadata.prediction_length,
context_length=dataset.metadata.prediction_length*2,
scaling=scaling,
hidden_dimension=2,
batch_size=batch_size,
num_batches_per_epoch=num_batches_per_epoch,
trainer_kwargs=dict(max_epochs=epochs)
)训练模型:
predictor = estimator.train(
training_data=train_dataset,
cache_data=True,
shuffle_buffer_length=1024
)
>>> INFO:pytorch_lightning.callbacks.model_summary:
| Name | Type | Params
---------------------------------------
0 | model | DLinearModel | 4.7 K
---------------------------------------
4.7 K 可训练参数
0 不可训练参数
4.7 K 总参数
0.019 总估计模型参数大小(MB)
Training: 0it [00:00, ?it/s]
...
INFO:pytorch_lightning.utilities.rank_zero:Epoch 49, global step 5000: 'train_loss' was not in top 1
INFO:pytorch_lightning.utilities.rank_zero:`Trainer.fit` stopped: `max_epochs=50` reached.在测试集上进行评估:
from gluonts.evaluation import make_evaluation_predictions, Evaluator
forecast_it, ts_it = make_evaluation_predictions(
dataset=dataset.test,
predictor=predictor,
)
d_linear_forecasts = list(forecast_it)
d_linear_tss = list(ts_it)
evaluator = Evaluator()
agg_metrics, _ = evaluator(iter(d_linear_tss), iter(d_linear_forecasts))因此,DLinear模型的结果为:
dlinear_mase = agg_metrics["MASE"]
print(f"DLinear MASE: {dlinear_mase:.3f}")
>>> DLinear MASE: 0.965与之前一样,我们通过以下辅助函数绘制训练的DLinear模型的预测结果:
def plot_gluonts(index):
plt.plot(d_linear_tss[index][-4 * dataset.metadata.prediction_length:].to_timestamp(), label="target")
d_linear_forecasts[index].plot(show_label=True, color='g')
plt.legend()
plt.gcf().autofmt_xdate()
plt.show()
plot_gluonts(4)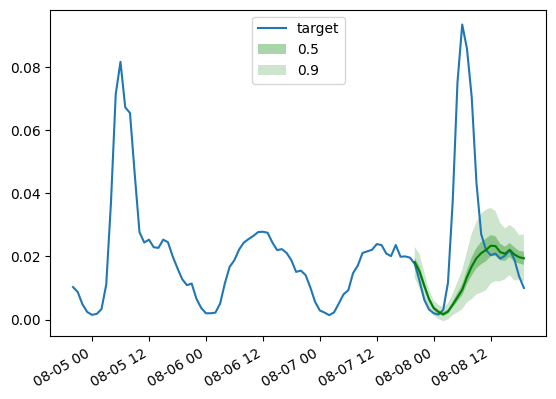
traffic数据集在工作日和周末的传感器模式之间存在分布偏移。这里发生了什么?由于DLinear模型无法融合协变量,特别是任何日期时间特征,我们给它的上下文窗口没有足够的信息来确定预测是周末还是工作日。因此,模型将预测更常见的模式,即工作日,导致在周末的性能较差。当然,通过给它一个更大的上下文窗口,线性模型将能够找出每周的模式,但也许数据中存在着更大的月度或季度模式,这将需要越来越大的上下文。
结论
基于Transformer的模型与上述线性基准模型相比如何?我们拥有的不同模型的测试集MASE指标如下:
可以看到,我们去年介绍的普通Transformer在这里取得了最好的结果。其次,多变量模型通常比单变量模型更差,原因是难以估计交叉序列的相关性/关系。估计值添加的额外方差通常会损害最终的预测结果,或者模型学习到了虚假的相关性。最近的论文,如CrossFormer(ICLR 23)和CARD,试图解决Transformer模型中的这个问题。多变量模型通常在大量数据上训练时表现良好。然而,与单变量模型相比,特别是在较小的开放数据集上,单变量模型往往提供更好的指标。通过将线性模型与等效大小的单变量Transformer或实际上任何其他神经网络单变量模型进行比较,通常可以获得更好的性能。
总结一下,当涉及到时间序列预测时,变压器绝对不会过时!然而,大规模数据集的可用性对于发挥它们的潜力至关重要。与计算机视觉(CV)和自然语言处理(NLP)不同,时间序列领域缺乏公开可访问的大规模数据集。大多数现有的时间序列预训练模型是在UCR和UEA等存档中的小样本大小上进行训练的,这些存档只包含几千甚至几百个样本。尽管这些基准数据集对于时间序列社区的进展起到了重要作用,但它们有限的样本大小和缺乏普遍性给预训练深度学习模型的预训练提出了挑战。
因此,开发大规模通用的时间序列数据集(类似于计算机视觉中的ImageNet)至关重要。创建这样的数据集将极大地促进针对时间序列分析专门设计的预训练模型的进一步研究,并提高预训练模型在时间序列预测中的适用性。
致谢
我们衷心感谢Lysandre Debut和Pedro Cuenca在本项目中提供的深思熟虑的评论和帮助 ❤️。